Bayes’ Theorem, error and bias
What is the effect of using Bayes’ Theorem to combine multiple pieces of evidence, given the presence of error and bias in estimating the probabilities of evidence? Will the error grow or decrease as we add more evidence?
Tim Hendrix has claimed1 that Richard Carrier’s use of Bayes Theorem will cause errors in Carrier’s estimates to inflate. I find this counter-intuitive, because I believe Bayes’ Theorem is frequently used specifically to counter uncertainty in any of the individual parameters, giving us a best estimate of the overall probability. This, I believe, should counter uncertainty regardless of whether the cause is in the evidence itself, that is, we have some evidence that points in the wrong direction, or in our imperfect ability to estimate what a certain piece of evidence means.
The inputs are as follows:
P(ei|A): The probability that evidence ei would be observed if hypothesis A is correct.
P(ei|B): The probability that evidence ei would be observed if hypothesis B is correct.
Bayes’ Theorem also uses a prior probability, which is our prior estimate that hypothesis A is correct. In this case, I will use 0.5 for the prior, which means that we have no relevant information other than that contained in the evidence. Apart from this, we believe A and B to be equally likely.
The resulting formula as used by Carrier is 2:
P(A|e) = [ 0.5 * ∏ P(ei|A) ] / [ 0.5 * ∏ P(ei|A) + (1-0.5) * ∏ P(ei|B) ]
To find out what the effects of error are, I simulated a large number of cases. In each case, I varied the number of pieces of evidence from 1 to 50. I assumed that the correct estimate of P(ei|A) was always 0.6, while the correct estimate of P(ei|B) was always 0.75. That is, all evidence is in reality likely on hypothesis A, but still somewhat more likely on B. I chose these conditions so as to create a very tricky situation, where even modest errors or bias can lead us to the wrong conclusion.
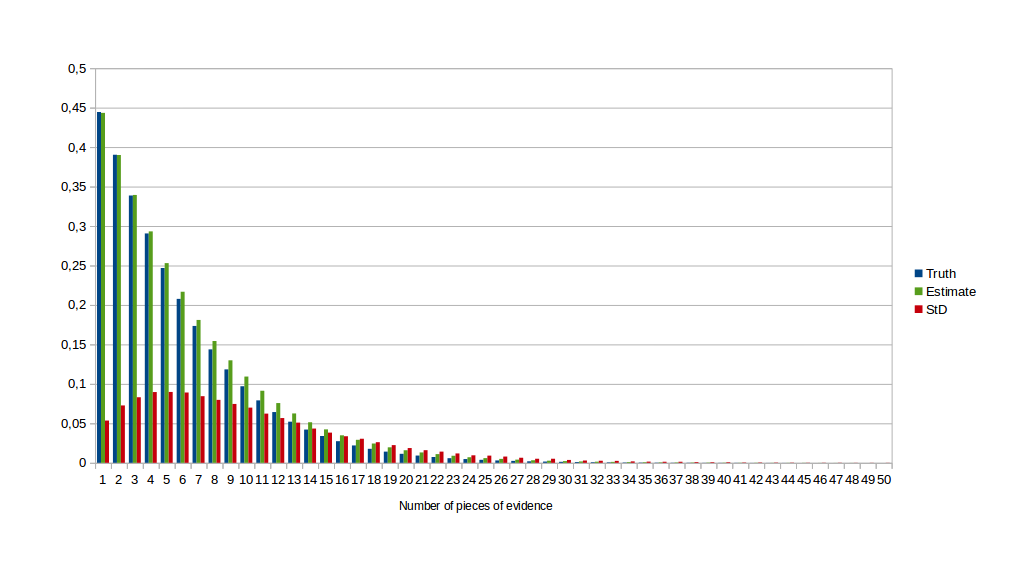
For the first experiment, I added a standard error of 0.1 and no bias. Below is the graph of the resulting probability of A given perfect estimates, the average resulting probability given imperfect estimates, and the standard deviation.
As we can see, when we add more pieces of evidence, the result using imperfect estimates gets closer and closer to the ideal.
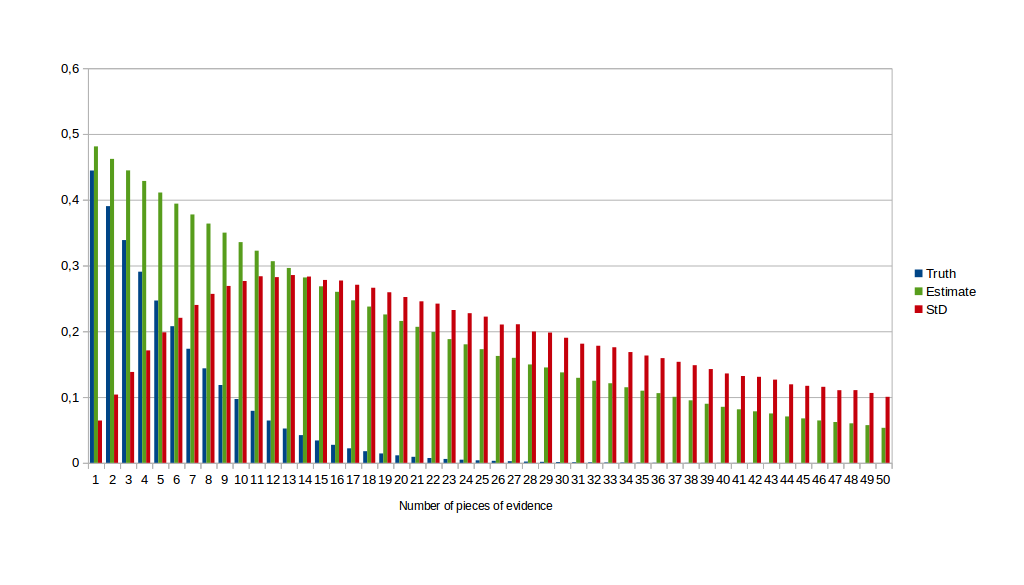
For the second experiment, I also added a bias of 0.05 in favour of A and -0.05 against B.
The presence of bias changes nothing fundamentally about the results. As we can see very clearly in this graph, the standard deviation first increases because the ideally computed probability approaches zero faster than when we add flaws to our estimates.
The conclusion from the experiment is that Bayes’ Theorem, as used by Carrier, appears to reduce rather than inflate errors.
This obviously does not mean that Carrier’s conclusions are correct. If his errors and bias are sufficiently large, he will reach the wrong conclusions. That is true regardless of any method he uses. However, I cannot think of a method that would give a better result in this case. For instance, one alternative would be to use only the ‘best’ single piece of evidence. This would translate to using the piece of evidence that according to our imperfect estimate would result in the clearest outcome. It is obvious that this would lead to much worse results. In part because, as we see, adding more evidence brings us closer to the correct conclusion. But also because our error and bias may easily lead us to choose the wrong ‘best’ piece of evidence.
Tim Hendrix
November 21, 2016 - 02:11
Well, I am sure that is all true, however, I hope you can see it is not actually related to what I say about OHJ as you are not using Carrier’s probabilities. If you make a similar experiment using Carrier’s actual computation you will see that I am correct.
Johan Rönnblom
March 20, 2017 - 19:10
We can’t use Carrier’s numbers because we do not know what the correct evaluation is. We could of course assume that Carrier is correct, but then the calculation becomes very one-sided since Carrier’s numbers are overwhelmingly in support of myth.
I think it is more instructive to look at a situation where the evidence is less decisive. Of course, many would argue that Carrier’s judgement is wrong and that the evidence is closer to 50/50, or clearly in favor of historicity. That is a different argument, here I am simply examining what happens when we have a situation where the evidence is close to 50/50 in either direction. It is really in this situation where we need Bayes, because in a more clear cut case we can intuitively see where the evidence is leading us.